Поздовжні і поперечні хвилі
Відвернемося від внутрішньої будови речовини для того, щоб досліджувати закони поширення механічних хвиль. Речовина будемо розглядати як суцільне середовище, безперервно змінюється в просторі.
Часткою, вивчаючи коливання, будемо називати малий елемент об'єму середовища, розміри якого значно більше, ніж відстані між молекулами, при цьому частку середовища приймаємо за матеріальну точку.
Розглядаючи механічні хвилі, будемо вважати речовини, в яких вони поширюються, пружними, внутрішні сили, що виникають в них при малих деформаціях, пропорційними величині деформації.
При порушенні коливання, в якому-небудь місці пружного середовища, в результаті взаємодії частинок середовища, воно поширюється в речовині від точки до точки з деякою кінцевою швидкістю. Процес поширення коливань називають хвилею. Важливою властивістю хвильового процесу є те, що в ньому не відбувається перенесення маси, кожна частка виконує коливання біля положення рівноваги. В хвилі від частки до частки передається стан коливального руху і енергія коливань. Хвиля переносить енергію.
Залежно від напрямку коливань частинки речовини по відношенню до напрямку поширення хвилі, хвилі ділять на поздовжні і поперечні.
поздовжні хвилі
визначення
Якщо частинки здійснюють коливання в напрямку поширення хвилі, то таку хвилю називаютьпоздовжньої.
Поздовжні хвилі поширюються в речовині, в якому виникають сили пружності, при деформації розтягування і стиснення в речовині в будь-якому агрегатному стані.
Так, наприклад, хвилі звуку, що поширюються в повітрі, відносять до поздовжніх хвилях. Поздовжні хвилі, що мають частоти від 17 до 20 ~ 000 Гц називають звуковими. Швидкість поширення акустичних хвиль залежить від властивостей середовища і її температури.
При поширенні поздовжньої хвилі в середовищі виникають чергування згущень і розрідження частинок, що переміщаються в напрямку поширення хвилі зі швидкістю $ v $. Весь час існування хвилі, елементи середовища виконують коливання у своїх положень рівноваги, при цьому різні частинки здійснюють коливання із зсувом по фазі. У твердих тілах швидкість поширення поздовжніх хвиль більше, ніж швидкість поперечних хвиль.
Швидкість поширення поздовжніх пружних хвиль в однорідних в газах або рідинах дорівнює:
\ [V = \ sqrt {\ frac {K} {\ rho}} \ left (1 \ right), \]
де $ K $ - модуль об'ємної пружності речовини; $ \ Rho = const $ - щільність середовища. У газах формула (1) справедлива, якщо надлишковий тиск багато менше, ніж рівноважний тиск невозмущенного газу.
Швидкість поширення поздовжніх хвиль в тонкому стрижні, викликаних його поздовжнім розтягом і стисненням дорівнює:
\ [V = \ sqrt {\ frac {E} {\ rho}} \ left (2 \ right), \]
де $ E $ - модуль Юнга речовини стержня.
поперечні хвилі
визначення
Поперечною хвилею називають таку хвилю, в якій коливання частинок середовища відбуваються в напрямках перпендикулярних до напрямку поширення хвилі.
Механічні хвилі можуть бути поперечними тільки в середовищі, в якій можливі деформації зсуву (середовище має пружністю форми). Отже, в рідинах і газах механічних поперечних хвиль не спостерігають. Поперечні механічні хвилі виникають в твердих тілах. Прикладом таких хвиль є хвилі, які розповсюджуються в натягнутих струнах.
Швидкість ($ v $) поширення поперечних хвиль у нескінченній ізотропному середовищі можна обчислити як:
\ [V = \ sqrt {\ frac {G} {\ rho} \ left (3 \ right),} \]
де $ G $ - модуль зсуву середовища; $ \ Rho $ - щільність речовини.
Пружні властивості і щільність твердого тіла залежить від хімічного складу речовини, і вона несуттєво змінюється при зміні тиску і температури. Тому в більшості випадків швидкість поширення хвилі можна вважати постійною.
Наведена тут швидкість поширення пружних хвиль називається фазовою швидкістю.
Рівняння поздовжньої і поперечної хвилі
Основним завданням при вивченні хвиль є встановлення закону зміни в часі і просторі фізичних величин, які однозначно характеризують рух хвилі. При розгляді пружних хвиль такою величиною служить, наприклад, зміщення ($ s $) частинок середовища від їх положень рівноваги. Функція $ s $ в залежності від координат простору і часу називається рівнянням хвилі.
Найпростішим видом хвиль є гармонійні хвилі. В таких хвилях параметри $ s $ для всіх частинок середовища, які охоплені хвилею, здійснюють гармонійні коливання з однаковими частотами. Для реалізації даного хвильового процесу необхідно, щоб джерело гармонійних хвиль здійснював незгасаючі гармонійні коливання.
Рівняння одновимірної хвилі записують як:
\ [S = A {\ cos \ left [\ omega t-kx + \ varphi \ right] \} \ left (4 \ right). \]
де
\ [K = \ frac {2 \ pi} {\ lambda} = \ frac {\ omega} {v} \ left (5 \ right), \]
$ K $ - хвильове число; $ \ Lambda \ $ - довжина хвилі; $ A $ - амплітуда хвилі в точці (якщо середовище не поглинає енергію, то амплітуда коливань збігається з амплітудою коливань джерела хвиль); $ \ Left [\ omega t-kx + \ varphi \ right] $ - фазою хвилі; $ \ Omega $ - циклічна частота коливань; $ \ Varphi $ - початкова фаза.
Приклади завдань з рішенням
приклад 1
Завдання: Поперечна хвиля поширюється по натягнутій струні зі швидкістю $ v = 2 \ frac {м} {з} $, період коливань точок струни дорівнює T = 1 с, амплітуда коливань становить 0,05 м. Якими будуть зміщення і швидкість малого елемента струни , який знаходиться на відстані $ x_1 = 1 \ $ м від джерела коливань в момент часу $ t_1 $ = 2 c?
Рішення: Основою для вирішення завдання служить рівняння одномірної хвилі:
\ [S = A {\ cos \ left [\ omega t-kx \ right] \} \ left (1.1 \ right), \]
де $ s $ - зміщення точки струни, що здійснює коливання; $ X $ - відстань від джерела хвилі до розглянутої точки; $ K = \ frac {\ omega} {v} $ - хвильове число; $ V $ - швидкість поширення хвилі.
Циклічну частоту $ \ omega $ знайдемо (при T = 1 c) як:
\ [\ Omega = \ frac {2 \ pi} {T} = 2 \ pi (\ frac {радий} {з}) \ left (1.2 \ right). \]
Тоді хвильове число при $ v = 2 \ frac {м} {з} $ одно:
\ [K = \ frac {2 \ pi} {2} = \ pi (\ frac {1} {м}). \]
Рівняння для нашої хвилі в урахуванням даних завдання набуде вигляду:
\ [S = 0,05 {\ cos \ left [2 \ pi t- \ pi x \ right] \} \ \ left (1.3 \ right). \]
Зсув точки струни, що знаходиться на відстані $ x_1 = 1 \ $ м від джерела коливань в момент часу $ t_1 $ = 2 c дорівнюватиме:
\ [S_1 = 0,05 {\ cos \ left [2 \ pi \ cdot 2 \ pi \ cdot 1 \ right] \} = - 0,05 \ \ left (м \ right). \]
Швидкість даної точки струни знайдемо як:
\ [\ Frac {ds} {dt} \ left (t_1, \ x_1 \ right) = - 0,1 \ pi {\ sin \ left [2 \ pi t- \ pi x \ right] \} = - 0, 01 \ pi {\ sin \ left [4 \ pi - \ pi \ right] = \} 0 \ \ left (\ frac {м} {з} \ right). \]
Відповідь: $ s_1 = -0,05 $ м; $ \ Frac {ds} {dt} \ left (t_1, \ x_1 \ right) $ = 0 $ \ frac {м} {з} $
приклад 2
Завдання: Плоска одномірна хвиля поширюється в пружною середовищі. Зобразіть на графіку напрямок швидкості частинок середовища в точках $ s = 0, \ $ при t = 0 для поздовжньої і поперечної хвиль.
Рішення: Рівнянням одновимірної плоскої хвилі служить вираз:
\ [S = A {\ cos \ left [\ omega t-kx \ right] \} \ left (2.1 \ right). \]
При $ t = 0 \ c $ з виразу (2.1) отримуємо:
\ [S = A {cos \ left [kx \ right] \} \ left (2.2 \ right). \]
У поздовжньої хвилі частинки зміщуються вздовж напрямку швидкості руху хвилі (рис.1).
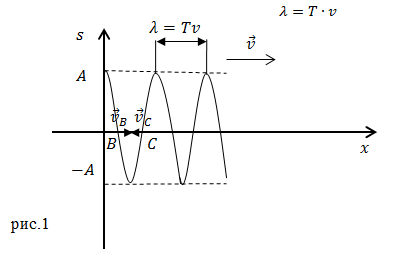
У поздовжньої хвилі частинки здійснюють коливання поперек напрямку швидкості руху хвилі рис.2.
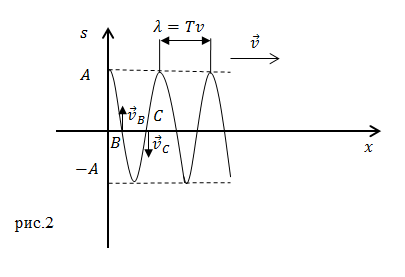
Читати далі: прямолінійний рівноприскореному русі .
Якими будуть зміщення і швидкість малого елемента струни , який знаходиться на відстані $ x_1 = 1 \ $ м від джерела коливань в момент часу $ t_1 $ = 2 c?